Hello all! I originally planned to make this post a short video, but after filming an hour-long explanation of lesson 1.3, I made the decision to think realistically about the aesthetic, and emotional appeal of over an hour of explanation of linear algebra! So instead….a quick article.
Last week, my meeting with Dr. Prudhom centered primarily around really building up a better understanding of the geometry of vectors. The book gave this example…
You are given a vector: [1, 3, -1], and you must find the vector that is perpendicular to it. The book generously gives us a method for this, explaining that the dot product method can help one find the perpendicular of a vector (the dot product is an equation that multiplies: x_1(v_1)+x_2(v_2)+x_3(v_3)) and so on and so forth ad finitem). To find the perpendicular to a vector you set this equation to zero, so in this case we would have: 0=x_1(1)+x_2(3)+x_3(-1). Our goal is to find what x_1, x_2, and x_3 are, because these are the components of the perpendicular vector. For the purposes of clarity, I changed x_1, x_2, and x_3 into x, y, and z.
Here is the first method that one can solve this problem with:

This is the way that I attempted to solve the problem before meeting with Dr. Prudhom. The issue with what I did was that I tried to solve for each variable in terms of the others. In other words, I solved for x in terms of y and z, y in terms of x and z, and z in terms of x and y. I then put these expressions into vector form: you’ve probably guessed my mistake: I ended up with the same number of variables as I started with! When we solve for systems of arbitrary size, the goal is always to come away having decreased the number of variables from when you started. The correct operation, is to choose ONE variable to solve for in terms of the others: I chose z. Then when I wrote the vector representation of the solution I had only two variables that I was dealing with, which was the closest that we could come to finding a solution.
The second method that Dr. Prudhom showed me unlocked something in my brain regarding geometrical representations of vectors:
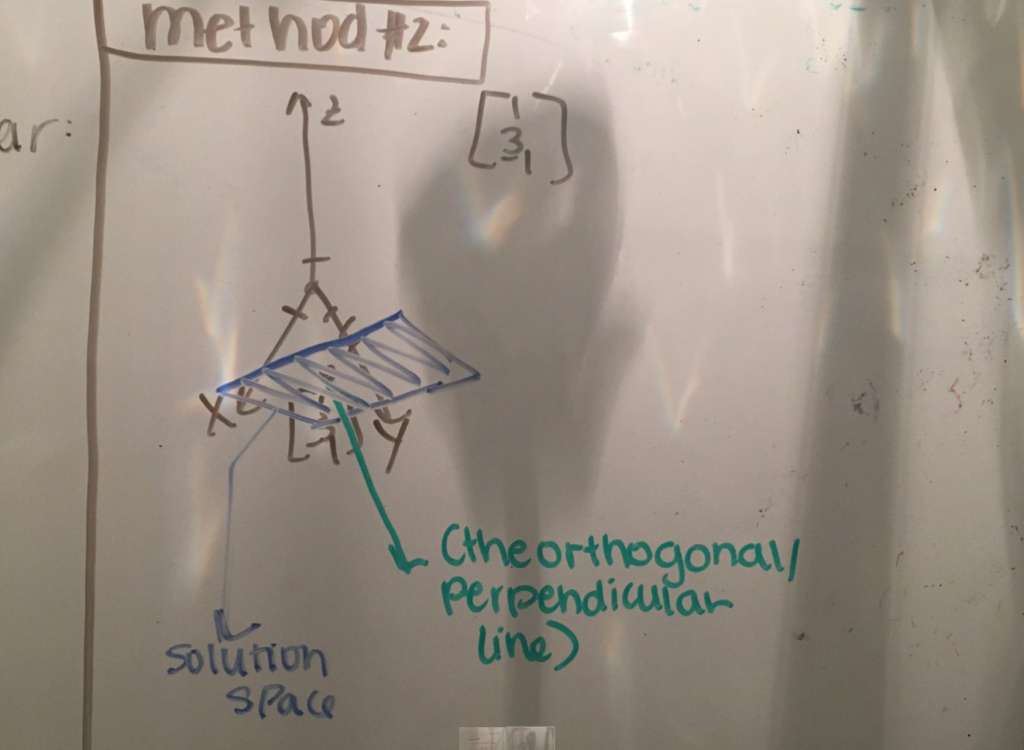
First, we drew the x, y, z, space. This represents the plane along which the vector [1, 3, -1] lies. We plotted the vector: over 1 on the x, over 3 on the y, down 1 on the z. Then we thought about the possible solutions to the equation that we were working with: 0=x+3y-z. This equation takes place in a 3D space (x, y, z), as stated. But Dr. Prudhom explained one crucial law: the dimensions of the solution set of an equation are one less than the dimensions spanned by the variables in the original equation; in other words, the solution set to this equation would be two dimensional. Then we (meaning the royal we…pretty sure Dr. Prudhom already knew) brainstormed what an infinite 2D surface would look like. After taking far too long to realize that it would be a plane, we set about drawing this infinite plane on the x, y, z space. We drew a line coming out of the original vector that we had been given, and thought about how a plane would be positioned to be perpendicular to it. The drawing that you see here is that plane.
The most amazing thing that I realized was when I connected the two methods: the law that Dr. Prudhom gave me stated that the solution space had to be one less than the space spanned by the original variables: 2D. But in other words…you end up with two variables. That was exactly what we discovered in method one. The final vector that we wrote was in terms of two variables, whereas the original was three. For me, this connection unlocked an understanding of vectors that (hopefully) will serve me going forward. Anyway, just wanted to share that with you all!
