Here are three videos that break up lesson 2.4 into (slightly) more manageable chunks

lesson 2.4 beginning

Hello all! So one of the reasons that I post such in depth videos is for myself; it is helpful to go back and look at them. But I recognize that a lot of people do not have that kind of time…so what I am doing now is releasing two posts: one with videos, and one with a general blog article about my experience over and week that is a lot more general, and a lot less mathy!

Weekly Post for People that Don’t want to Watch Long Videos About Math…(So in Other Words…Videos for most people…)

Okay, so sarcastic title aside, I have been brainstorming ways to make this blog more accessible, and easier to just jump into without a big time commitment. I really want to focus on talking about general life lessons that I have learned from this experience, so each week I am going to focus on some general academic takeaways. This week there were several. I will also talk a bit about the questions that I have..

Time management over vacations: 

One of the biggest struggles of this independent study is balancing the video posts with the content: figuring out how to keep questions in my mind but still charge ahead with content and not get behind. This week was spring break, and what I noticed is that I had a lot of questions, but I still had to continue with new chapters. I also had to balance making videos with the very concrete issue of being in a very small hotel room and respecting other people’s sleep schedules :). What was helpful was really focusing on this week’s videos because it reminded me of my questions, and gave me a review of all the content that I covered over the week. 

Reading Advanced Textbooks..

This is a theme that has popped up over the course of this experience in general, but figuring out how to read advanced texts often comes down to reading VERY carefully. For example this week I was given the definition: 

image(f)={f(x): xin X}

={b in Y: b=f(x), for some x in X}. 

This definition is not hard once you break it down, but advanced texts really rely on abbreviations, quickly introducing variables, and rapidly moving through prerequisite knowledge of other proofs: you often have to slow WAY down and cross reference old proofs, say things out loud, write things out, and revisit things. All of these methods have helped, so that when I read this definition this week I was able to figure it out a lot more quickly than I could have at the beginning of this study. 

How to Teach and Be Engaging: 

This week hopefully marks the start of my most successful teaching experience. I have managed to find software that lets me digitally write on a whiteboard, I have cut down the videos into shorter, more frequent posts, and this post marks the start of my weekly, more general updates. One of the biggest problems for me so far has been how to share educational content in a way that moves quickly but is still interesting. While this does not have to do specifically with my topic, one thing that I have learned is how much time and energy it takes to teach, especially to teach in a less traditional format. I have a lot more respect now for the people that make things like crashcourse, and khan academy videos!

Specifics Matter!

The biggest thing that I learned this week was in regards to lesson 3.1 specifically. This lesson introduces the idea of image and kernel of a function: my immediate reponse was that image was the same thing as range, and kernel the same thing as domain, and I used this as a way to ground the new definitions in my mind. However, I actually discovered that there are some differences: my biggest question from this chapter was what those differences are, but this plays into a general theme that I have noticed in advanced mathematics: specifics matter, and definitions get nuanced…really nuanced. That means that you have to pay a lot of attention, and REALLY focus on wording. A lot of the proofs in linear algebra are similar to each other, but when you look closely they are proving two totally different things. Hopefully recognizing this idea now will set me up to success in future advanced courses. 

All right, well that is all that I have for this week. Hopefully this gave you some idea of some of the bigger takeaways that I have had. At the end of the day, content matters less than experience in an independent study: it is about learning how to learn, how to work through problems, and how to get out of your comfort zone, and this is my way of addressing that aspect of the course. 

-Taylor 

Finally, I wanted to share an example of the kind of prep that I do before I make my videos..

https://docs.google.com/document/d/1jvDp3fGSCn84bBrJSjluKU8ErxFxiPmwOBRi8-QOEO8/edit?usp=sharing

This document is the prep that I wrote down before doing the second part of my lesson 3.1 video; This is to help cut down on pauses, and confusion! If you’ve seen videos, you will likely notice that it doesn’t fix everything though! I think another challenge is not getting myself confused when I have to make a video on a topic that I still have a couple of questions on. Another challenge is that even when I write prep, it’s still a lot to remember for a video because there are often SO many proofs, examples, and definitions that I have to get through per lesson! If you do glance at this doc, please note that I only put it in here to show my process: it is all gibberish shorthand to another person so please don’t waste time trying to understand my incoherent thoughts 🙂

https://www.youtube.com/watch?v=iY158XiysEg

https://youtu.be/N78-eVbih2Y

*some theorems, laws, and rules that I find helpful to have written out for reference 🙂

Algebraic rules for A(vector x): A(vector x+ vector y)=A(vector x) + A(vector y)

A(k(vector x))=k(A(vector x))

matrix form of linear system: A(vector x)=vector b

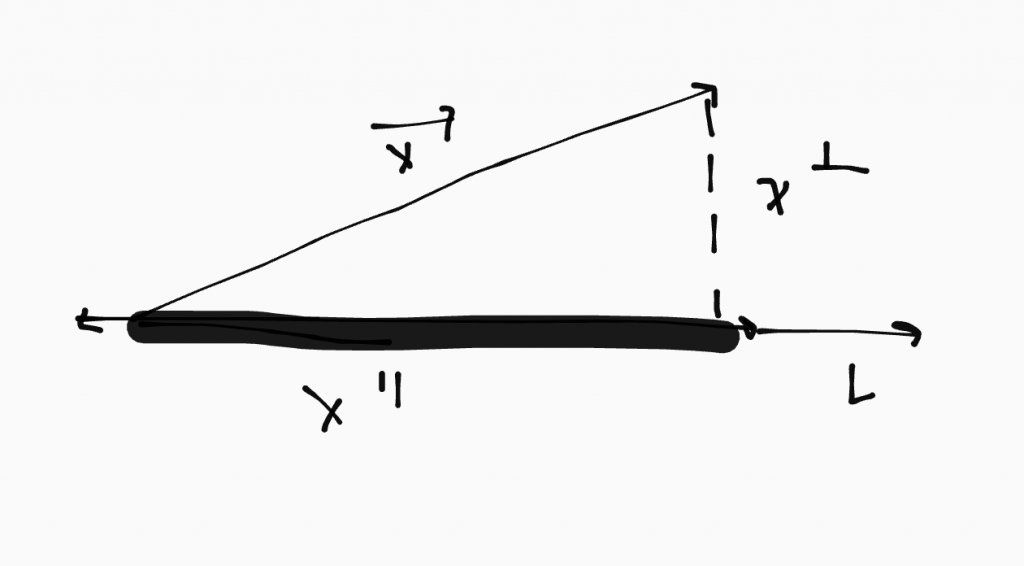
Lesson 2.2

1. vector x=the vector parallel to L(x ||) + the vector perpendicular to L (x _|_)
2. orthogonal projections: proj(L)(vector x)=x || *the orthogonal projection of the vector x onto the line L
3. Therefore: T(x)=x ||
4. x ||=k(vector w) *vector w=a vector that is on the same line as our transformation
5. vector x-k(vector w)=perpendicular to line L *bc (x _|_)=vector x-x||=vector x-k(vector w)
6. use the dot product method: (vector x-k(vector w)) (vector w)=0
7. if we distribute the w: (vector x times vector w) -k(vector w times vector w)=0
8. use this to solve for just k: (vector x)(vector w) / (vector w)(vector w)
9. then to circle all the way back to T(x) : since it equals k(vector w): that means that our general equation is…T(x)= ((vector x)(vector w) / (vector w)(vector w))*vector W, for an orthogonal projection
10. keep in mind that if we changed all of the w’s to the unit vector u (|vector u|=1) then the equation could be simplified: it would become; (vector x times vector u)(vector u)
11. The matrix for orthogonal projection:

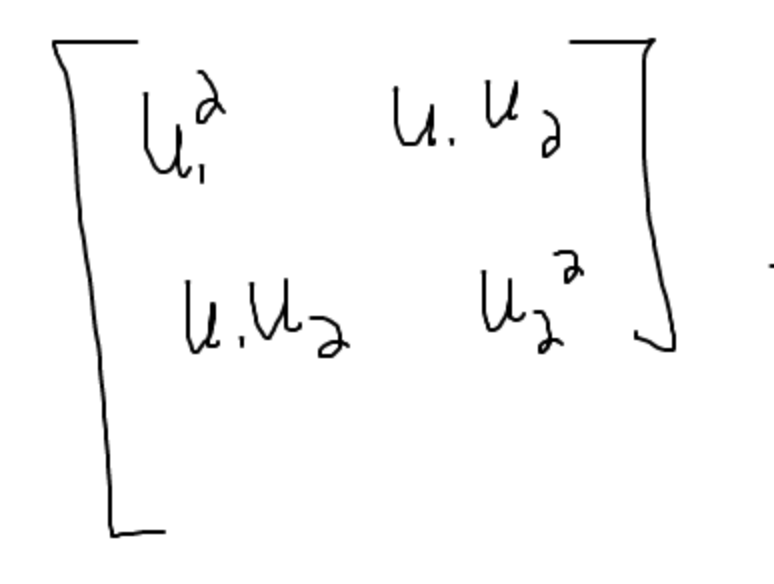
12) matrix for reflection(I won’t go through the whole proof like I did for orthogonal):

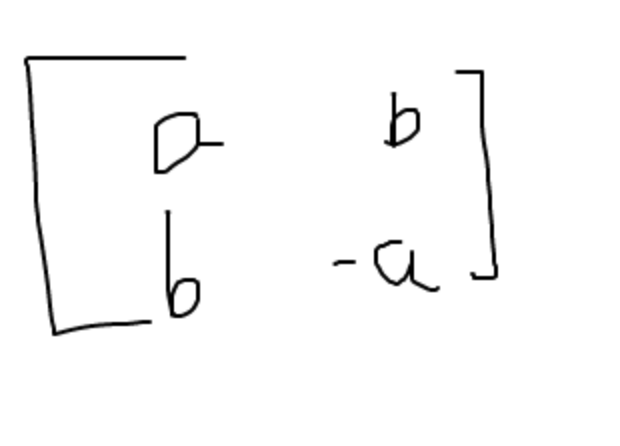
If a^2+ b^2=1

13) matrix for rotation:

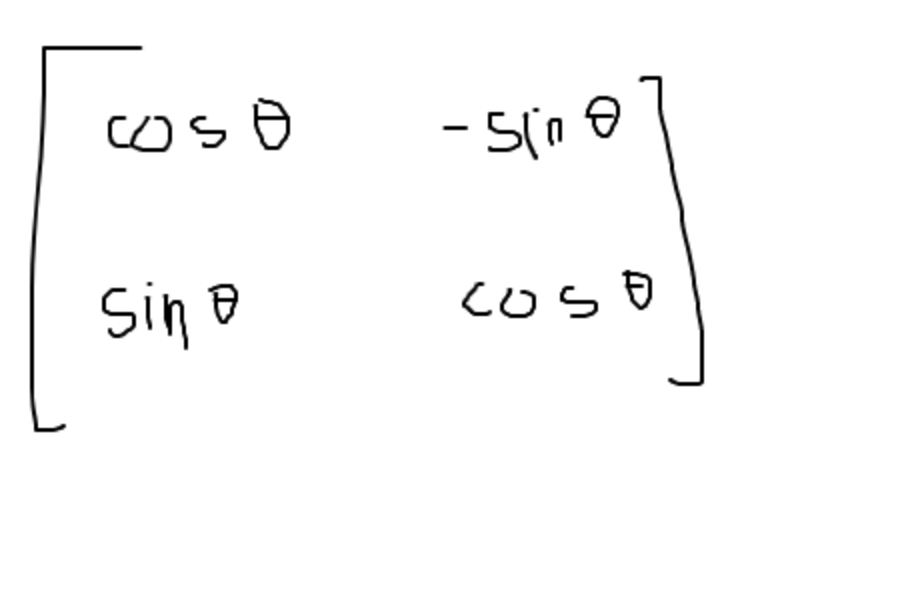
14) horizontal + vertical shear:

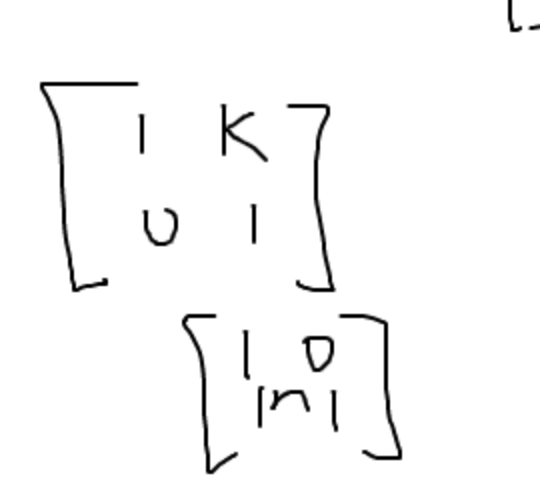
15) for invertibility: set the matrix equal to an identity matrix

16) standard vectors: the vectors that lie on the line of one axis.

Hello all! Here are my weekly videos: I will say, one thing that I noticed watching through is that the screen is REALLY hard to see: I am going to try to rectify this by sending out a written post tomorrow explaining in words a lot of what was discussed, and next week I will make sure to position the camera so that it is more easy to see!

So I took a different approach this week: here are three short videos on the chapter: while skipping around will make it harder to understand: I think that you can kind of skim or pick which ones you want to see, and still get a good feel for the chapter:

Video One: https://youtu.be/ORqd90gyNMI

Video Three

Example problems from lesson 1.3 (the end of the chapter!)

• I cut down the length a lot, so hopefully the video is a little less daunting
• https://www.youtube.com/watch?v=weAflAfgEys

If you don’t want to sit through this whole thing, the video is really split up into two parts. The first one ends around minute 20. And at the end of the day the most important part of Part two are the two equations listed at the end (the video is really just the context and explanations that make those equations make sense!)