*some theorems, laws, and rules that I find helpful to have written out for reference 🙂
Algebraic rules for A(vector x): A(vector x+ vector y)=A(vector x) + A(vector y)
A(k(vector x))=k(A(vector x))
matrix form of linear system: A(vector x)=vector b
Lesson 2.2
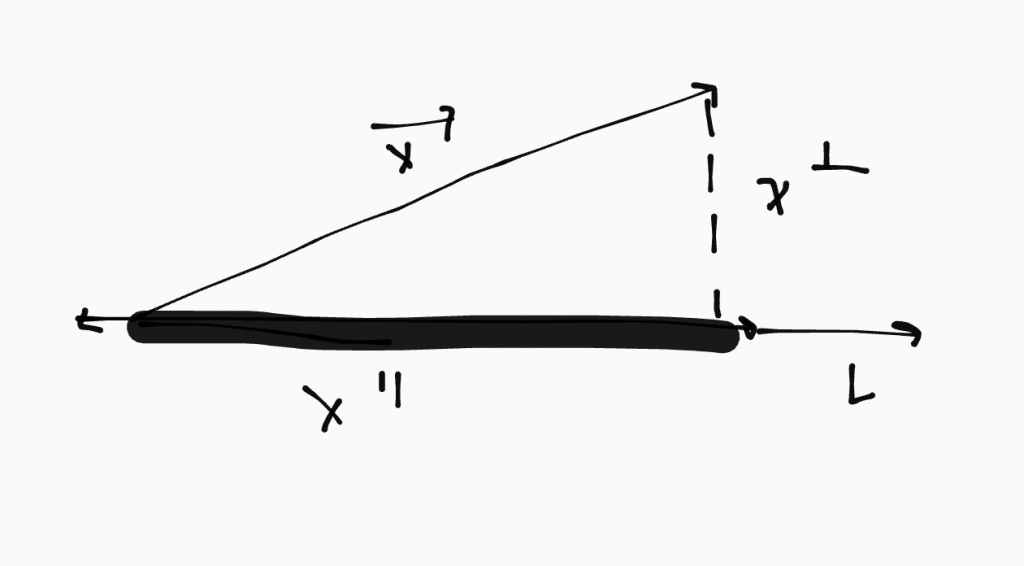
- vector x=the vector parallel to L(x ||) + the vector perpendicular to L (x _|_)
- orthogonal projections: proj(L)(vector x)=x || *the orthogonal projection of the vector x onto the line L
- Therefore: T(x)=x ||
- x ||=k(vector w) *vector w=a vector that is on the same line as our transformation
- vector x-k(vector w)=perpendicular to line L *bc (x _|_)=vector x-x||=vector x-k(vector w)
- use the dot product method: (vector x-k(vector w)) (vector w)=0
- if we distribute the w: (vector x times vector w) -k(vector w times vector w)=0
- use this to solve for just k: (vector x)(vector w) / (vector w)(vector w)
- then to circle all the way back to T(x) : since it equals k(vector w): that means that our general equation is…T(x)= ((vector x)(vector w) / (vector w)(vector w))*vector W, for an orthogonal projection
- keep in mind that if we changed all of the w’s to the unit vector u (|vector u|=1) then the equation could be simplified: it would become; (vector x times vector u)(vector u)
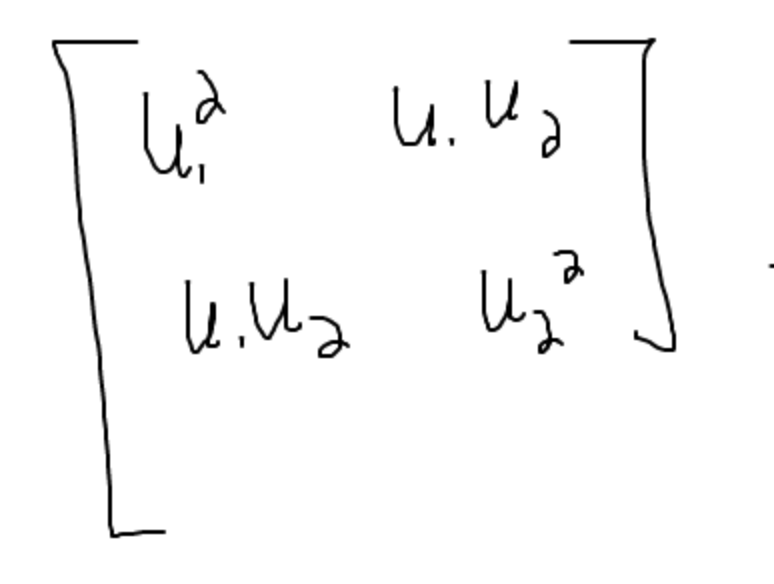
- The matrix for orthogonal projection:
12) matrix for reflection(I won’t go through the whole proof like I did for orthogonal):
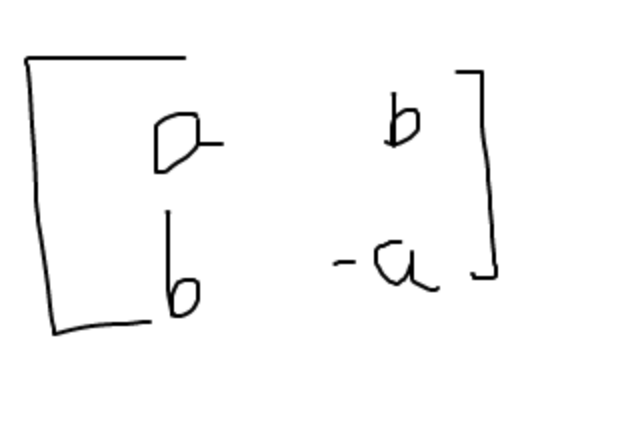
If a^2+ b^2=1
13) matrix for rotation:
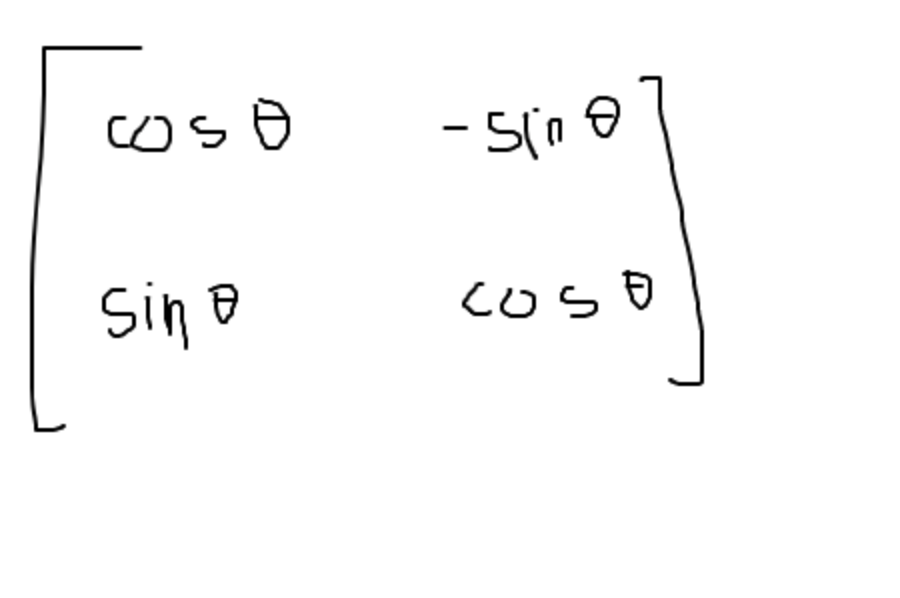
14) horizontal + vertical shear:
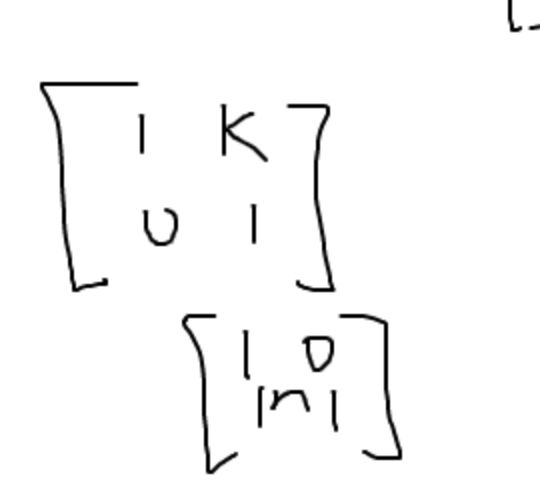
15) for invertibility: set the matrix equal to an identity matrix
16) standard vectors: the vectors that lie on the line of one axis.
